大数据培训_PCA降维

PCA（Principal Component Analysis，主成分分析）
在高维向量空间中，随着维度的增加，数据呈现出越来越稀疏的分布特点，增加后续算法的复杂度，而很多时候虽然数据维度较高，但是很多维度之间存在相关性，他们表达的信息有重叠。
PCA的思想是将n维特征映射到k维上(k<n)，这k维是全新的正交特征。
这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征（这也是与特征选择特征子集的方法的区别）。

PCA的目的是在高维数据中找到最大方差的方向，接着映射它到比最初维数小或相等的新的子空间。

​

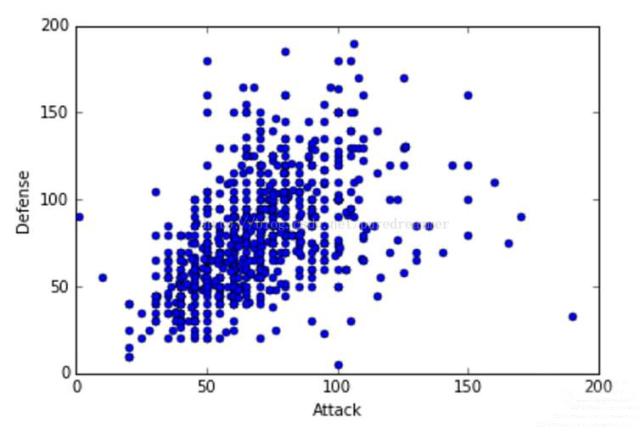
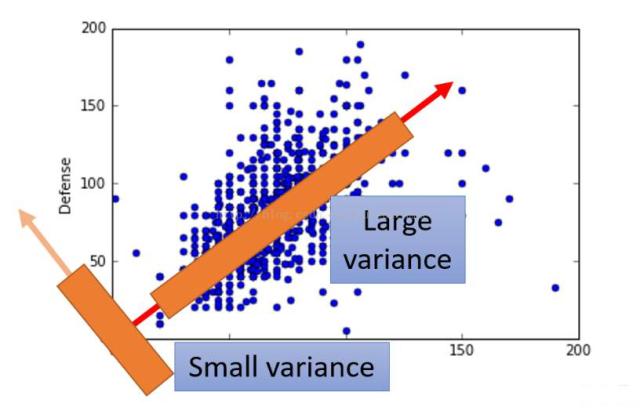
​PCA算法流程

输入：训练样本集 D=x(1),x(2),...,x(m)D=x(1),x(2),...,x(m) ,低维空间维数 d′d′ ;
过程：.
1：对所有样本进行中心化（去均值操作）： x(i)j←x(i)j?1m∑mi=1x(i)jxj(i)←xj(i)?1m∑i=1mxj(i) ;
2：计算样本的协方差矩阵 XXTXXT ;
3：对协方差矩阵 XXTXXT 做特征值分解 ;
4：取最大的 d′d′ 个特征值所对应的特征向量 w1,w2,...,wd′w1,w2,...,wd′
5：将原样本矩阵与投影矩阵相乘： X?WX?W 即为降维后数据集 X′X′。其中 XX 为 m×nm×n 维， W=[w1,w2,...,wd′]W=[w1,w2,...,wd′] 为 n×d′n×d′ 维。
6：输出：降维后的数据集 X′
PCA算法分析
优点：使得数据更易使用，并且可以去除数据中的噪声，使得其他机器学习任务更加精确。该算法往往作为预处理步骤，在数据应用到其他算法之前清洗数据。
缺点：数据维度降低并不代表特征的减少，因为降维仍旧保留了较大的信息量，对结果过拟合问题并没有帮助。不能将降维算法当做解决过拟合问题方法。如果原始数据特征维度并不是很大，也并不需要进行降维。