学分高考 IT技术

大数据培训_朴素贝叶斯分类

发布时间: 2022-03-18 11:09:01

大数据培训_朴素贝叶斯分类

什么是贝叶斯算法
朴素贝叶斯是最常用的两种分类算法。贝叶斯定理是以英国数学家贝叶斯命名，用来解决两个条件概率之间的关系问题。简单的说就是在已知P(A|B)时如何获得P(B|A)的概率。朴素贝叶斯（Naive Bayes）假设特征P(A)在特定结果P(B)下是独立的。

概率基础

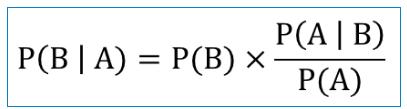
在开始介绍贝叶斯之前，先简单介绍下概率的基础知识。概率是某一结果出现的可能性。例如，抛一枚匀质硬币，正面向上的可能性多大？概率值是一个0-1之间的数字，用来衡量一个事件发生可能性的大小。概率值越接近1，事件发生的可能性越大，概率值越接近0，事件越不可能发生。我们日常生活中听到最多的是天气预报中的降水概率。概率的表示方法叫维恩图。下面我们通过维恩图来说明贝叶斯公式中常见的几个概率。

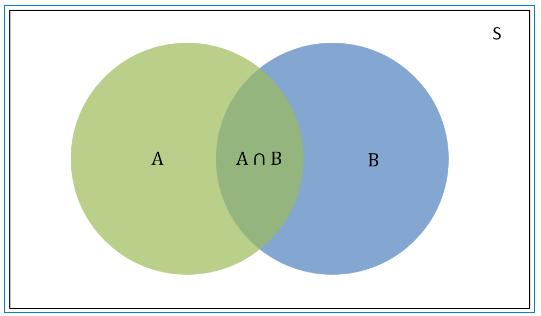
在维恩图中：
S：S是样本空间，是所有可能事件的总和。
​P(A)：是样本空间S中A事件发生的概率，维恩图中绿色的部分。
​P(B)：是样本空间S中B事件发生的概率，维恩图中蓝色的部分。
​P(A∩B)：是样本空间S中A事件和B事件同时发生的概率，也就是A和B相交的区域。
​P(A|B)：是条件概率，是B事件已经发生时A事件发生的概率。

贝叶斯算法通过已知的P(A|B)，P(A),和P(B)三个概率计算P(B|A)发生的概率。假设我们现在已知P(A|B)，P(A)和P(B)三个概率，如何计算P(B|A)呢？通过前面的概率树及P(A|B)的概率可知，P(B|A)的概率是在事件A发生的前提下事件B发生的概率，因此P(B|A)可以表示为事件B与事件A的交集与事件A的比率。
​

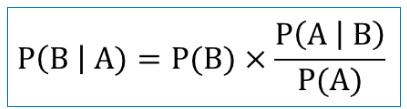
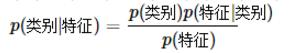
在贝叶斯推断中，每一种概率都有一个特定的名字：
​P(B)是”先验概率”(Prior probability)。
​P(A)是”先验概率”(Prior probability)，也作标准化常量(normalized constant)。
​P(A|B)是已知B发生后A的条件概率，叫做似然函数(likelihood)。
​P(B|A)是已知A发生后B的条件概率，是我们要求的值，叫做后验概率。
​P(A|B)/P(A)是调整因子，也被称作标准似然度（standardised likelihood）。
​

解决问题
下面从一个简单问题出发，介绍怎么使用朴素贝叶斯解决分类问题。
一天，老师问了个问题，只根据头发和声音怎么判断一位同学的性别。
为了解决这个问题，同学们马上简单的统计了7位同学的相关特征，数据如下：​

头发

声音

性别

长

粗

男

短

粗

男

短

粗

男

长

细

女

短

细

女

短

粗

女

长

粗

女

长

粗

女

​

这个问题之前用决策树做过了，这里我们换一种思路。
要是知道男生和女生头发长短的概率以及声音粗细的概率，我们就可以计算出各种情况的概率，然后比较概率大小，来判断性别。
假设抽样样本足够大，我们可以近似认为可以代表所有数据，假设上位7位同学能代表所有数据，这里方便计算~
由这7位同学，我们马上得出下面表格概率分布。

概率分布​

性别

头发长

声音粗

男

1/3

1

女

3/5

3/5

假设头发和声音都是独立特征，于是
男生头发长声音粗的概率=3/8*1/3*1=1/8
女生头发长声音粗的概率=5/8*3/5*3/5=9/40
因为1/8<9/40所以如果一个人，头发长，声音粗，那么这个人更可能是女生，于是出现这些特征就是女生。其他特征依次类推。
这就是朴素贝叶斯分类方法。是的，就是这么简单。
下面来解释原理，先看贝叶斯公式：

​​

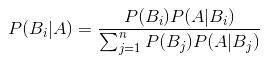
公式中，事件Bi的概率为P(Bi)，事件Bi已发生条件下事件A的概率为P(A│Bi)，事件A发生条件下事件Bi的概率为P(Bi│A)。
带入我们的例子中，判断头发长的人性别：
P(男|头发长)=P(头发长|男)*P(男)/P(头发长)
P(女|头发长)=P(头发长|女)*P(女)/P(头发长)
判断头发长、声音粗的人性别：
P(男|头发长声音粗)=P(头发长|男)P(声音粗|男)*P(男)/P(头发长声音粗)
P(女|头发长声音粗)=P(头发长|女)P(声音粗|女)*P(女)/P(头发长声音粗)
可以看到，比较最后比较概率，只用比较分子即可。也就是前面计算头发长声音粗的人是男生女生的概率。
​

朴素贝叶斯分类的工作流程​

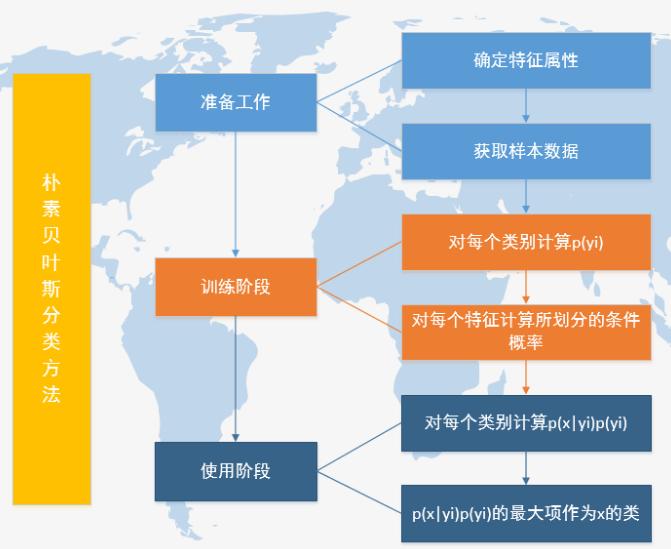
朴素贝叶斯python实例​

实例内容​

假设有两类数据p1(x,y)表示（x,y）属于类别1，用p2(x,y)表示（x,y）属于类别2，那么对于一个新的数据集（x,y），可以根据一下规则来判断他的类别

1.如果p1(x,y)>p2(x,y)，则（x,y）属于类别1

2.如果p2(x,y)>p1(x,y)，则（x,y）属于类别2

也就是说，我们会选择具有最高概率的决策，这就是贝叶斯决策理论的核心思想通常，事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件下的概率是不一样的；然而，这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。作为一个规范的原理，贝叶斯法则对于所有概率的解释是有效的；然而，频率主义者和贝叶斯主义者对于在应用中概率如何被赋值有着不同的看法：频率主义者根据随机事件发生的频率，或者总体样本里面的个数来赋值概率；贝叶斯主义者要根据未知的命题来赋值概率。一个结果就是，贝叶斯主义者有更多的机会使用贝叶斯法则。

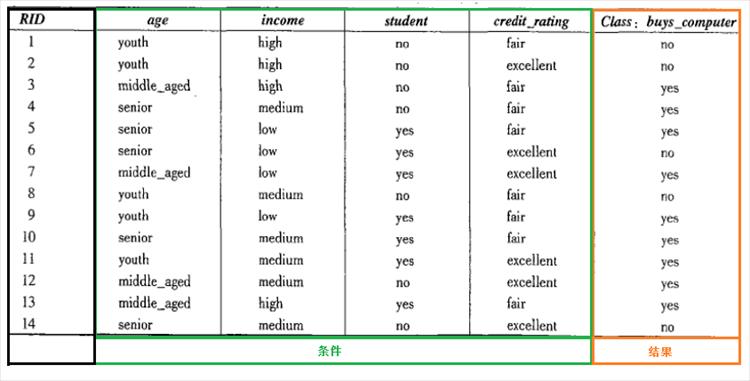
14个里面有5个不买电脑，9个买电脑。
p(age=youth|buy_computer=yes) = 2/9 =0.222
p(age=youth|buy_computer=no) = 3/5 = 0.6

p(student=yes|buy_computer=yes) = 6/9 =0.667
p(student=yes|buy_computer=no) = 1/5 = 0.2

p(age=senior & student=yes|buy_computer=yes) = 2/3 =0.667
p(age=senior & student=yes|buy_computer=no) = 1/3 = 0.333


Python代码

class NBClassify(object):

def __init__(self,fillNa = 1):

self.fillNa = 1

pass

def train(self,trainSet):

# 计算每种类别的概率

# 保存所有tag的所有种类，及它们出现的频次

dictTag = {}

for subTuple in trainSet:

dictTag[str(subTuple[1])] = 1 if str(subTuple[1]) not in dictTag.keys() else dictTag[str(subTuple[1])] + 1

# 保存每个tag本身的概率

tagProbablity = {}

totalFreq = sum([value for value in dictTag.values()])

for key,value in dictTag.items():

tagProbablity[key] = value / totalFreq

# print(tagProbablity)

self.tagProbablity = tagProbablity

##############################################################################

# 计算特征的条件概率

# 保存特征属性基本信息{特征1:{值1:出现5次,值2:出现1次},特征2:{值1:出现1次,值2:出现5次}}

dictFeaturesbase = {}

for subTuple in trainSet:

for key,value in subTuple[0].items():

if key not in dictFeaturesbase.keys():

dictFeaturesbase[key] = {value:1}

else:

if value not in dictFeaturesbase[key].keys():

dictFeaturesbase[key][value] = 1

else:

dictFeaturesbase[key][value] += 1

# dictFeaturesbase = {

# '职业': {'农夫': 1,'教师': 2,'建筑工人': 2,'护士': 1},

# '症状': {'打喷嚏': 3,'头痛': 3}

# }

dictFeatures = {}.fromkeys([key for key in dictTag])

for key in dictFeatures.keys():

dictFeatures[key] = {}.fromkeys([key for key in dictFeaturesbase])

for key,value in dictFeatures.items():

for subkey in value.keys():

value[subkey] = {}.fromkeys([x for x in dictFeaturesbase[subkey].keys()])

# dictFeatures = {

# '感冒 ': {'症状': {'打喷嚏': None,'头痛': None},'职业': {'护士': None,'农夫': None,'建筑工人': None,'教师': None}},

# '脑震荡': {'症状': {'打喷嚏': None,'头痛': None},'职业': {'护士': None,'农夫': None,'建筑工人': None,'教师': None}},

# '过敏 ': {'症状': {'打喷嚏': None,'头痛': None},'职业': {'护士': None,'农夫': None,'建筑工人': None,'教师': None}}

# }

# initialise dictFeatures

for subTuple in trainSet:

for key,value in subTuple[0].items():

dictFeatures[subTuple[1]][key][value] = 1 if dictFeatures[subTuple[1]][key][value] == None else dictFeatures[subTuple[1]][key][value] + 1

# print(dictFeatures)

# 将驯良样本中没有的项目，由None改为一个非常小的数值，表示其概率极小而并非是零

for tag,featuresDict in dictFeatures.items():

for featureName,feturevalueDict in featuresDict.items():

for featureKey,featurevalues in feturevalueDict.items():

if featurevalues == None:

feturevalueDict[featureKey] = 1

# 由特征频率计算特征的条件概率P(feature|tag)

for tag,featuresDict in dictFeatures.items():

for featureName,feturevalueDict in featuresDict.items():

totalCount = sum([x for x in feturevalueDict.values() if x != None])

for featureKey,featurevalues in feturevalueDict.items():

feturevalueDict[featureKey] = featurevalues/totalCount if featurevalues != None else None

self.featuresProbablity = dictFeatures

##############################################################################

def classify(self,featureDict):

resultDict = {}

# 计算每个tag的条件概率

for key,value in self.tagProbablity.items():

iNumList = []

for f,v in featureDict.items():

if self.featuresProbablity[key][f][v]:

iNumList.append(self.featuresProbablity[key][f][v])

conditionPr = 1

for iNum in iNumList:

conditionPr *= iNum

resultDict[key] = value * conditionPr

# 对比每个tag的条件概率的大小

resultList = sorted(resultDict.items(),key=lambda x:x[1],reverse=True)

return resultList[0][0]

if __name__ == '__main__':

trainSet = [

({"症状":"打喷嚏","职业":"护士"},"感冒 "),

({"症状":"打喷嚏","职业":"农夫"},"过敏 "),

({"症状":"头痛","职业":"建筑工人"},"脑震荡"),

({"症状":"头痛","职业":"建筑工人"},"感冒 "),

({"症状":"打喷嚏","职业":"教师"},"感冒 "),

({"症状":"头痛","职业":"教师"},"脑震荡"),

]

trainSet = [

({"age":"youth","收入":"高","学生":"no","信用":"fair"},"不买"),

({"age":"youth","收入":"高","学生":"no","信用":"excellent"},"不买"),

({"age":"midden_aged","收入":"高","学生":"no","信用":"fair"},"买"),

({"age":"senior","收入":"中等","学生":"no","信用":"fair"},"买"),

({"age":"senior","收入":"低","学生":"yes","信用":"fair"},"买"),

({"age":"senior","收入":"低","学生":"yes","信用":"excellent"},"不买"),

({"age":"midden_aged","收入":"低","学生":"yes","信用":"excellent"},"买"),

({"age":"youth","收入":"中等","学生":"no","信用":"fair"},"不买"),

({"age":"youth","收入":"低","学生":"yes","信用":"fair"},"买"),

({"age":"senior","收入":"中等","学生":"yes","信用":"fair"},"买"),

({"age":"youth","收入":"中等","学生":"yes","信用":"excellent"},"买"),

({"age":"midden_aged","收入":"中等","学生":"no","信用":"excellent"},"买"),

({"age":"midden_aged","收入":"高","学生":"yes","信用":"fair"},"买"),

({"age":"senior","收入":"中等","学生":"no","信用":"excellent"},"不买")

]

monitor = NBClassify()

# trainSet is something like that [(featureDict,tag),]

monitor.train(trainSet)

# 打喷嚏的建筑工人

# 请问他患上感冒的概率有多大？

# result = monitor.classify({"症状":"头痛","职业":"教师"})

result = monitor.classify({"age":"midden_aged","收入":"高","学生":"yes","信用":"excellent"})

print(result)

​朴素贝叶斯优缺点
优点：在数据较少的请胯下仍然有效，可以处理多类别问题；
缺点：对于输入数据的准备方式较为敏感。
使用数据类型：标称型数据

温馨提示：
本文【大数据培训_朴素贝叶斯分类】由作者教培参考提供。该文观点仅代表作者本人，学分高考系信息发布平台，仅提供信息存储空间服务，若存在侵权问题，请及时联系管理员或作者进行删除。
IT行业真的好找工作吗？
hcie路由交换认证考试，你了解这些吗？
相关阅读
教培参考
教育培训行业知识型媒体
相关I T
网络工程师好找工作吗
网页微信缓存的视频在哪个文件夹
ascii是什么编码
md5是加密算法吗
md5码是什么意思
ajax的原理
转过账的好友删了能加回来吗
FPTOcr是什么软件
路由器reset是什么意思
et是什么文件
教育资讯
1
湖南2025年高考报名将于2024年10
2
2024软科中国高职院校排名出炉
3
2024年全国高校名单大全(3117所)
4
2024胡润百学全球高中排行榜发布
5
2024年全国高考拉开帷幕
6
教育部发布2024年高考十问十答
7
学位法通过，2025年1月1日起施行
8
全国教育辟谣平台正式上线
9
2024三位一体招生政策有哪些变化
10
中考体育改革后首次现场考试下月
我们采用的作品包括内容和图片部分来源于网络用户投稿，我们不确定投稿用户享有完全著作权，根据《信息网络传播权保护条例》，如果侵犯了您的权利，请联系我站将及时删除。
内容侵权、违法和不良信息举报
Copyright @ 2024 学分高考 All Rights Reserved 版权所有. 湘ICP备17021685号