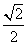
题已知直线的极坐标方程为,则极点到这条直线的距离是( )。
题目详情:
已知直线的极坐标方程为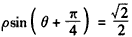 ,则极点到这条直线的距离是( )。
,则极点到这条直线的距离是( )。
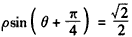 ,则极点到这条直线的距离是( )。
,则极点到这条直线的距离是( )。
答试题答案
为你推荐
-
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°。解:(解法一):(1)设AC与BD交于O,连结PO。 ∵底面ABCD是菱形,∴BD⊥AC,∵PA⊥底面ABCD,BD平面ABCD,∴PA⊥BD,又PA∩AC=A,∴BD⊥平面PAC。

-
参数方程x=3-2ty=-1-4t(t为参数)所表示的曲线是( )A.直线B.圆C.椭圆D.双曲线把参数方程x=3-2ty=-1-4t(t为参数)消去参数,化为普通方程为 2x-y-7=0,表示一条直线,故选A.

-
已知直线l:x=1y=1+t(t为参数)的倾斜角是( )A.π6B.π4C.π3D.π2化参数方程为普通方程,可得x=1,则直线的斜率不存在,故倾斜角为π2.故选D.

-
已知点P是曲线C:x=4cosθy=3sinθ(θ为参数,0≤θ≤π)上一点,O为原点.若直线OP的倾斜角为π4,则点P的直角坐标为 ______.将曲线C:x=4cosθy=3sinθ的一般方程为x216+y29=1 (y>0) ①∵O为原点,直线OP的倾斜角为π4,∴直线OP的方程为y=x ②联立①②可得x=y=125∴点P的直角坐标为

-
直线y=2x+1的参数方程是( )A.x=t2y=2t2+1(t为参数)B.x=t-1y=2t-1(t为参数)C.x=2t-1y=4t+1(t为参数)D.x=sinθy=2sinθ+1(θ为参数)∵y=2x+1,∴y+1=2(x+1),令x+1=t,则y+1=2t,可得x=t-1y=2t-1(t为参数),即为直线y=2x+1的参数方程.故选B.














